이 글을 보시는 분들 모두에게 먼저 정말 미리미리 당부 드립니다.
로또 당첨번호는 정말 무작위의 번호 추첨이기 때문에 규칙이란게 없습니다.
한번 뽑은 숫자공이 제외되는 것도 아니고
매번 뽑을때마다 매번 새로운 경우의 수이기 때문에
규칙을 찾거나 예측을 한다는거 자체가 불가능한 영역입니다.
만약 정말 만약 우리가 모르는 어떠한 힘에 의해 규칙이 있다고 해도
이제 겨우 950회가 넘는 로또 회차로는 표본이 너무 적어
정확한 데이터 모델링도 예측을 하기도 어렵습니다.
그러니 부디!! 이 글은 그저 선형회귀라는게 이런거구나 정도로만 봐주시고
얘는 어떤 뻘짓을 이렇게 정성들여서 하나 재미로 봐주시기 바랍니다.
물론 모델을 만들어서 진짜 로또 당첨되면 저야 좋지만
그럴 확률은 길가다가 당첨 복권을 줍는거랑 똑같은 이치기에
저는 그냥 선형회귀에 대해서 공부하고 하나의 프로젝트를 해보고 싶어
단순히 학습목적으로 활용해 보는것임을 미리 알려드립니다.
시작
서론이 길었지만 말한대로 로또 당첨번호에는 규칙이 없다.
그렇지만 선형회귀모델에 대해 공부해보고 응용해보고 싶은데
머신러닝 단에서 마땅히 써볼만한 곳이 생각이 안나서
꾸역꾸역 갖다 쓰는 정도이기 때문에 목적성 보다는
그 내용에 중점을 두고 프로젝트를 진행하고자 한다.
선형회귀란
본 프로젝트 시작에 앞서 선형회귀가 무엇인지 알아야
왜 이 프로젝트를 하고 왜 선형회귀를 쓰는지 알 수 있을것이다.
선형회귀(線型回歸), 한자어 그대로 해석해 보면은
'선의 형태로 돌아가다'고 할 수 있겠다.
말 그대로 종속변수 Y와 한 개 이상의 독립변수 X에 대해
둘의 관계를 선으로 나타내는 회귀분석의 기법니다.
한개의 설명 변수에 기반한 경우는 단순 선형 회귀
둘 이상의 설명 변수에 기반한 경우는 다중 선형 회귀라 한다.
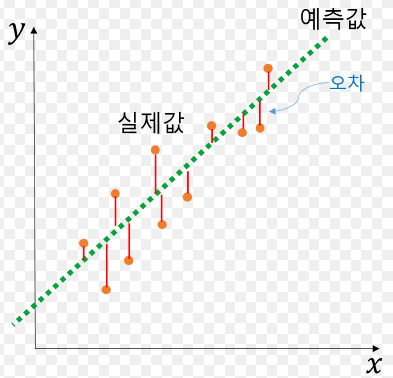
단순 선형 회귀를 예로 들어서 설명하자면,
위의 그림에서 보이는 빨간 점이 우리가 가지고 있는 x와 y의 관계
쉽게 말하면 데이터라고 할 수 있겠다.
선형 회귀의 시작은 이 데이터들을 평면에 표시했을때
모든 점들을 지나는 선이 존재할 것이다는 전제에서 시작한다.
물론 모든 점들을 지나는 선이 존재할 수도 있고 아닐 수도 있다.
만약 그런 선이 존재하지 않는다면 선으로 부터 점들의 거리가
가장 적게 떨어져 있는(오차가 적은) 이상적인 선을 찾고자 하는 것이다.
로또로의 적용
이런 선형회귀 모델을 로또에 생각하게 된 건
로또는 회차(x)가 존재하고 6개의 번호가 존재한다.
6개의 번호 a,b,c,d,e,f에 대해 y로 본다면은
6개의 선형회귀 모델을 이용해 어떤 선을 그릴수 있지 않을까
라는 생각에서 시작하게 되었다.
쉽게 말해 (x, a)에 대한 선형모델로 첫번째 번호를
(x, b)에 대한 선형모델로 두번째 번호를 예측하는 식이다.
여기서 반드시 깔려야 하는 전제 조건은 a<b이다.
로또 당첨번호 6개 수는 맨 앞이 작은 수인 오름차순 정렬이다.
그러니까 이에 맞추어 프로그래밍을 진행해야 할 것이다.
(너무 당연한 얘기지만서도...)
추가로 모델이 잘 나온다면은(정답률 50% 이상)
번호 등장 빈도에 따라 값을 다르게 주어서
정답률 향상까지 진행해보고자 한다.
데이터 셋 구하기
dhlottery.co.kr/gameResult.do?method=allWinPrint&gubun=byWin&nowPage=&drwNoStart=848&drwNoEnd=899
로또 공식 홈페이지에 가면은 회차별 당첨번호 조회 하단에서
원하는 회차부터 회차까지 당첨내역을 엑셀로 받을 수 있다.
머신러닝에 학습시킬 데이터는 여기서 받은 엑셀파일로 진행하겠다.
일단 데이터는 확보 됐으니 다음 글에서는
데이터 전처리 과정을 다뤄보도록 하겠다.
※다시 한번 말하지만 로또 번호는 예측이란게 안됩니다.
저는 단순 공부차원에서 데이터로 활용하는 겁니다.
'인공지능 > 머신러닝' 카테고리의 다른 글
| [머신러닝] 결정트리 (1) | 2024.07.31 |
|---|---|
| [머신러닝] 머신러닝의 3가지 학습 방법 (2) | 2021.06.18 |
| [머신러닝] 선형회귀모델을 이용한 로또 번호 예측하기 - 3(모델링) (1) | 2021.05.16 |
| [머신러닝] 선형회귀모델을 이용한 로또 번호 예측하기 - 2(데이터) (1) | 2021.04.07 |



